مقدمه

برای بیان فرمولبندی «قوانین انتشار نور»، نیاز به تعریف مجموعه‌ای از مفاهیم اولیه است که در اینجا به آنها می‌پردازیم. این مفاهیم اولیه عبارتند از:

• محیط‌ انتشار نور
• ضریب شکست
• محیط خلاء
• رنگ نور
• پاشندگی
• همگنی محیط
• همسانگردی محیط
• مرز جدایی محیط‌ها
• مفهوم پرتو
• مفهوم باریکه و انواع آن
• مفهوم جبهه
• صفحه تابش

انتشار نور

انتشار نور در فضا در‌ واقع انتشار نور در محیط‌های فیزیکی و توسطِ این محیط‌هاست. از نظر فیزیکی، نور در زمان انتشار با محیط برهمکنش می‌کند. میزان این برهمکنش به ویژگی‌های نور و همینطور خصوصیات محیط ربط دارد. برای مشخص کردن بزرگی برهمکنش، عددی را به محیط نسبت می‌دهیم که از آن به عنوان «ضریب شکست» یاد می‌کنیم و با $n$ نمایش می‌دهیم. محیط فیزیکی‌ای که کمترین برهمکنش با نور را دارد، «خلاء» نامیده می‌شود و عدد ۱ را به عنوان ضریب شکست به آن نسبت می‌دهیم. هر چه برهمکنش بیشتر باشد، ضریب شکست محیط به همان نسبت بزرگتر از ۱ خواهد شد. عدد ضریب شکست محیط‌های متعارف معمولاً کمتر از ۲ است، اگر چه در بعضی از مواد مثل نیمه‌هادی‌ها با اعداد بزرگتری نیز مواجه می‌شویم. (محیط‌های آزمایشگاهی دست‌ساز با ساختارهای پیچیده هم داریم که ضریب شکست‌های بسیار بزرگ دارند.) از آنجایی که خلاء کمترین برهمکنش با نور را دارد، بدیهی است که نمی‌توان ضریب شکست کوچکتر از ۱ (از نظر قدر مطلق) داشت. باختصار اشاره کنیم که میزان برهمکنش به پارامترهای متعددی ربط دارد که ساختار فضایی ماده و ساختار مولکولی اجزای آن شاید مهمترین آنها باشد و در این بین چگالی جرمی محیط اهمیت چندانی ندارد.

علاوه بر این، برهمکنش نور و محیط به ویژگی‌های نور هم ربط دارد. یکی از ویژگی‌های مهم نور در اینجا چیزی است که از آن به عنوان «رنگ» یاد می‌کنیم. چشم انسان به این خصوصیت نور حساس است و آن را با دقت بالایی تفکیک می‌کند. بنابراین برای انسان مفهومی کاملاً آشناست. رنگ را با نماد $\lambda$ نشان داده و مقیاس‌بندی می‌کنند. به این خصوصیت «طول موج» نور هم می‌گویند (البته برای فهم ویژگی رنگ نیاز نیست حتماً مُدلی موجی را برای توصیف انتشار نور در نظر بگیریم). معمولاً رنگ را بر حسب واحد «متر» و آحاد آن بیان و اندازه‌گیری می‌کنند که در این حالت بیشتر از آن با نام طول‌موج یاد می‌شود و در واقع مدلی موجی برای توصیف نور در نظر گرفته شده است که در آن ملاک رنگ، طول‌موج نور در خلاء است. واحدهای دیگری که برای بیان رنگ استفاده می‌شود، واحدهای انرژی (مانند ژول) و فرکانس (هرتز) هستند. در این حالت نور به مثابهٔ ذره (فوتون) در نظر گرفته شده است. این مدل‌ها تقریباً بطور کامل در توصیف رنگ با هم سازگار هستند. صرفنظر از نوع مُدل استفاده شده برای توصیف نور، مفهوم «رنگ» ویژگی فیزیکی مهم نور و مفهومی اساسی است.

چشم انسان یکی از پیشرفته‌ترین آشکارسازهای نور است که قادر است شدت نور در محدودهٔ خاصی از رنگ‌ها را بسنجد. علاوه بر این چشم انسان قادر به تفکیک نور بر حسب ویژگی رنگ نیز هست.به این خاصیت چشم «دید رنگی» می‌گویند. محدودهٔ نوری را که چشم تشخیص می‌دهد، اصطلاحاً «نور مرئی» می‌نامند. قدرت سنجش شدت نور و نیز تفکیک رنگ در این ناحیه بسیار بالاست. ناحیهٔ مرئی، بطور تقریبی شامل طول‌موج‌های ۳۸۰ تا ۷۸۰ نانومتر است که به آن «طیف مرئی» نور می‌گویند. این طیف در تصویر زیر همراه با نمایش رنگی متناظر با دریافت و تعبیر فیزیولوژیکی چشم و مغز انسان دیده می‌شود.

با توجه به وابستگی میزان برهمکنش بین نور و محیط به رنگ نور، ضریب شکست تابعی از رنگ نور خواهد بود (یعنی $n=n(\lambda )$). این پدیده را «پاشندگی» می‌نامند. محیطی پاشنده است که رفتارش در برابر نور وابسته به رنگ نور باشد. خلاء، محیطی کاملاً غیرپاشنده است، یعنی ضریب شکست آن برای همهٔ رنگ‌های نور مساوی و برابر با ۱ است.

ضریب شکست یک محیط ممکن است در نقاط مختلف فضا تغییر کند، یعنی در حالت کلّی، $n=n(x,y,z)$. «محیط همگن»، محیطی است که میزان ضریب شکست آن در تمام نقاطش با هم برابر باشد. به همین ترتیب اگر ضریب شکست یک محیط در تمام جهات به یک شکل تغییر کند و تغییرات آن وابسته به جهت انتشار نور نباشد، محیطی «همسانگرد» خواهیم داشت. محیط «همگنِ همسانگرد»، محیطی است که ضریب شکست آن در تمام نقاط و در همهٔ جهات با هم برابر باشد. خلاء، محیطی کاملاً همگن و همسانگرد است. در محیط‌های دیگر ممکن است ضریب شکست بتدریج و بطور پیوسته در نقاط مختلف یا در جهات متفاوت تغییر کند. در یک محیط همگن و همسانگرد، ضریب شکست را می‌توان با یک کمیت نرده‌ای (اسکالر) نشان داد، اما در حالت کلی، چون با یک میدانِ ضریب شکستِ جهتدار مواجه هستیم، این کمیت در قالب ریاضی یک تانسور معرفی می‌شود. (البته در اینجا بطور ضمنی فرض شده بود که برهمکنش نور با محیط تنها منجر به انتقال یا انتشار نور در محیط می‌شود. اما در حالت واقعی‌تر، علاوه بر آن، تبدیل انرژی نورانی در پدیده‌هایی مانند جذب (انتقال یکطرفه انرژی نورانی به انرژی حالت مولکول) و تقویت (انتقال انرژی از مولکول به نور) نیز مشاهده می‌شود. برای گنجاندن این پدیده‌ها کافی است که ضریب شکست را با کمیتی مختلط نشان دهیم که بخش موهومی ضریب شکست (یا بخش موهومی عناصر تانسور آن) نشان‌دهنده جذب یا تقویت خواهد بود. این موضوع در اینجا محل بحث نیست.).

در مواردی ممکن است تغییرات ضریب شکست بصورت تیز و شدید باشد. یعنی در ناحیهٔ بسیار کوچکی از فضا، تغییر بزرگی در میزان ضریب شکست داشته باشیم. مثلاً اگر دو محیط با ضریب شکست متفاوت را در کنار هم قرار دهیم، (دو محیط که از آن‌ها با محیط ۱ و محیط ۲ یاد می‌کنیم)، تغییرات ضریب شکست در ناحیه‌ٔ انتقال از یک محیط به دیگری، بصورت ناگهانی و گسسته خواهد بود. به ناحیهٔ کوچکی که این تغییر در آن رخ می‌دهد، «مرز جدایی دو محیط» می‌گویند. این مرز جدایی توسط یک رویه یا سطح در فضا مشخص خواهد شد. در هندسه، رویه یا سطح با «بردار سطح» مشخص می‌شود. جهت این بردار، عمود بر سطح است. اگر مرز جدایی، یک سطح تخت باشد، جهت بردار سطح در تمام نقاط سطح ثابت و عمود بر سطح است. در غیر اینصورت، جهت بردار سطح در نقاط مختلف تغییر می‌کند.

انتشار نور در مواجهه با مرزهای جدایی تغییرات اساسی خواهد کرد. فرمولبندی‌های انتشار نور باید نحوهٔ تغییر در انتشار نور را در مواجهه با مرزهای جدایی به نحوی بیان کنند که با مشاهدات تجربی ما در این حالت سازگار باشند و مشخص کنند که وجود مرز، انتشار نور در هر یک از محیط‌های ۱ و ۲ را چگونه تغییر می‌دهد (البته مسئلهٔ نحوهٔ انتشار نور در خودِ مرز هم مهم است، اما در اپتیک هندسی به آن پرداخته نمی‌شود).

پرتو و باریکه

اگر یک منبع نقطه‌ای را در نظر بگیریم، طبق تعریف، نور آن در تمام جهات منتشر خواهد شد. می‌توان با قرار دادن مانع، عبور نور به یک ناحیه از فضا را محدود کرد. اگر در این مانع گسستگی یا شکافی باشد، نور از آن عبور خواهد کرد. در صورتی که این شکاف را کوچک کنیم، میزان نور عبوری و همینطور گستردگی آن محدود خواهد شد. با کم کردن متوالی قطر شکاف، به جایی می‌رسیم که نور خروجی تنها در یک راستا خارج می‌شود. در این حالت یک «پرتو»ی نور خواهیم داشت. اگر باز هم شکاف را کوچکتر کنیم، بر خلاف انتظار، نور مجدداً پخش می‌شود و اصطلاحاً پدیدهٔ پراش ظاهر خواهد شد (این پخش‌شدگی ناشی از اصل عدم قطعیت است)). بنابراین، پرتو، زمانی بدست می‌آید که بخش بسیار کوچکی از نور یک منبع را انتخاب کرده‌ایم امّا نه آنقدر کوچک که به ابعاد و محدودیت‌های پراش برسیم. یک پرتو نور در‌واقع کوچکترین خط فیزیکی ممکن است که در واقعیت به آن می‌توان رسید. اگر به جای یک شکاف، دو یا چند شکاف قرار دهیم، می‌توان چندین پرتو مختلف بدست آورد که هر کدام در راستای خاصی از فضا منتشر می‌شوند. با چند پرتوی نزدیک به هم یک «باریکهٔ نور» شکل می‌گیرد. باریکه، می‌تواند پهنای دلخواهی داشته باشد. در صورتی که پرتوهای یک باریکه همراستا باشند، باریکهٔ ما یک «باریکهٔ موازی» است (این حالت زمانی شکل می‌گیرد که در فاصلهٔ نسبتاً زیادی از منبع نور نقطه‌ای قرار داشته باشیم). در غیر اینصورت اگر پرتوهای باریکه موازی نباشند در بعضی از نقاط و جهتها ممکن است از هم دور شوند و یا ممکن است به هم نزدیک شوند. در این حالت می‌گوییم باریکه در آن ناحیه از فضا به ترتیب «باریکهٔ واگرا» یا «باریکهٔ همگرا» است. وضعیت «واگرایی» یک باریکهٔ نور در حین انتشار و عبور از محیط‌های مختلف ممکن است تغییر کند. مثلاً یک باریکهٔ‌ واگرا، ممکن است همگرا شده و سپس موازی گردد. اگر باریکه‌های نور به یک نقطه همگرا شوند، آن نقطه، می‌تواند جسم یا تصویر قلمداد شود. در‌واقع، این تعریف دیگری از جسم نورانی و تصویر آن است.

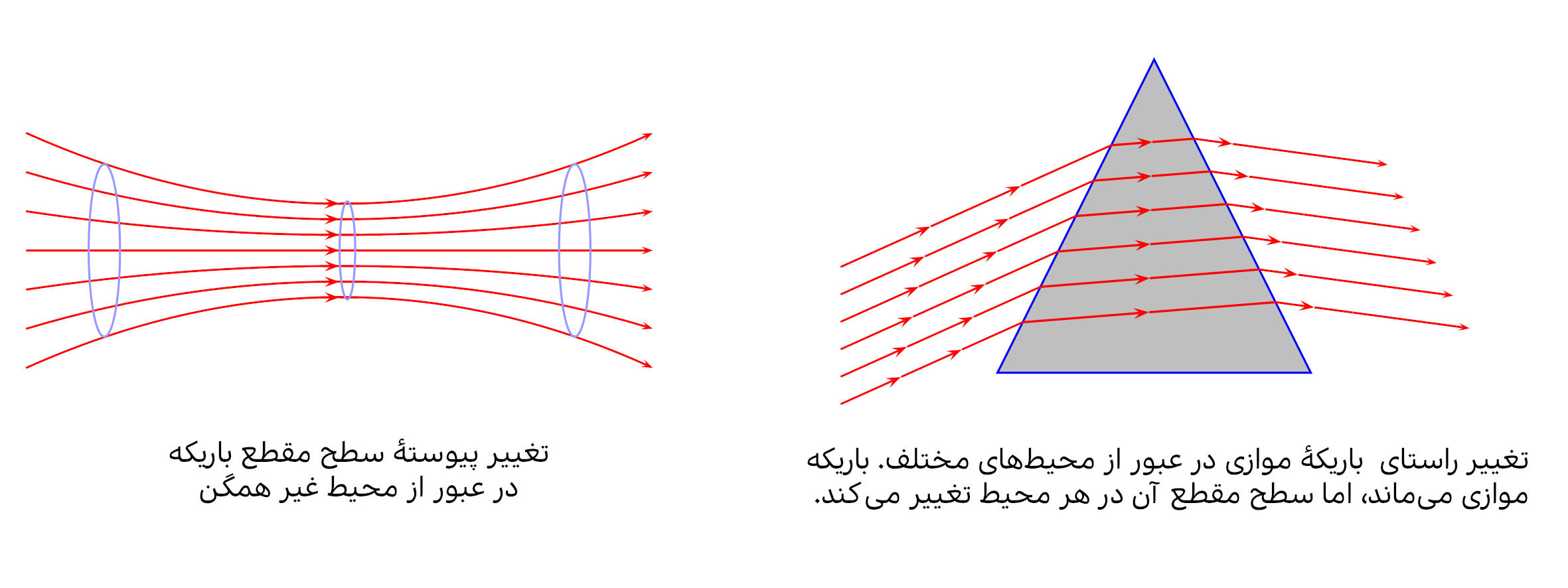
طبیعتاً سطح مقطع یک باریکهٔ همگرا و یا واگرا در حین انتشار تغییر می‌کند، امّا سطح مقطع یک باریکهٔ موازی هم لزوماً ثابت نیست. مثلاً ممکن است یک باریکهٔ موازی در یک نقطه از فضا سطح $A_1$ را داشته باشد، امّا پس از عبور از یک مرز جدایی، سطح آن به $A_2$ تغییر کند. از طرفی چون پرتوها و یا باریکه‌ها در فضای سه‌بُعدی منتشر می‌شوند، بنابراین ممکن است دو باریکه یا دسته پرتو در فضا همدیگر را قطع کنند و یا اینکه متنافر باشند، یعنی هیچگاه در هیچ نقطهٔ مشترکی از فضا قرار نگیرند.

برای توصیفِ ریاضی پرتوها و باریکه‌ها، می‌توان از مفهوم هندسی «خط» استفاده کرد (منظور حالت کلّی خط یا همان مسیر است نه صرفاً خطِ مستقیم). این خطوط در فضای سه‌بُعدی تعریف می‌شوند. به همین ترتیب، باریکه، مجموعه‌ای از خطوط با توزیع فضایی خاص است. اغلب برای نشان دادن پرتوها و باریکه‌ها، سطح مقطع برش آنها با یک صفحهٔ مشخص نشان داده می شود. با تغییر صفحهٔ برش‌دهنده، شکل باریکه در آن تغییر خواهد کرد. این بدان معناست که یک باریکه ممکن است در یک صفحه، همگرا ولی در صفحهٔ دیگر (مثلاً صفحهٔ عمود بر آن) واگرا باشد.

قبلاً اشاره کردیم که هیچ‌گاه نمی‌توان تمام انرژی نورانی یک جسم یا تصویر آن را دریافت کرد، چون در هر صورت، سیستمِ دریافت‌کننده دهانهٔ محدودی دارد (می‌خواهد چشم باشد یا دهانهٔ ورودی یک دوربین و یا سطح محدود یک آشکارساز). این دهانه، میدان دید محدودی دارد و زاویهٔ مشخصی از فضا را می‌بیند. بنابراین هر سیستم اپتیکی، تنها قادر به دریافت باریکه‌های نوری است نه کل تابش یک منبع و بسته به موقعیت و جهت‌گیری نسبی منبع و آشکارساز، سطح مؤثر باریکه ورودی فرق خواهد کرد، یعنی فقط بخشی از انرژی باریکهٔ ورودی را دریافت می‌کند.

جبهه

در هندسه، خط را به دو شکل می‌توان نمایش داد: روش اول نمایش نحوهٔ توزیع خط در فضا است. یعنی خط، چه نقاطی از فضای سه‌گانه را انتخاب می‌کند. معادلهٔ خط، این نقاط را در فضای سه‌بُعدی مشخص می‌کند. این بطور ساده همان کاری است که در رسم یک خط با خط‌کش (یا یک منحنی با شابلون) انجام می‌دهیم. امّا راه دوّم، معرفی جهت حداکثر تغییرات است. این کار با تعریف جهتِ عمود بر خط تعریف می‌شود. یعنی جهتی که اگر در امتداد آن حرکت کنیم، هیچ جابجایی در امتداد خط نخواهیم داشت. بنابراین جهتِ خط، یعنی جهت حداکثر تغییرات در راستای خط با طی کمترین مسیر و جهتِ عمود یعنی تغییرات صفر در آن راستا (در واقع تعریف تعامد این است). به عنوان مثال، اگر یک منبع نور نقطه‌ای داشته باشیم، پرتوهای آن، خطوطی شعاعی خواهند بود که از آن نقطه در فضا منتشر می‌شوند. اگر راستای عمود بر این خطوط را در یک فاصلهٔ معین از نقطهٔ منبع مشخص کنیم، یک سطح کروی حاصل می‌شود. در این مثال، روش اول با مجموعه‌ای از خطوط واگرا از یک نقطه در فضا و روش دوم با یک رویهٔ کروی به مرکزیت آن نقطه توزیع نور را نشان می‌دهد. در روش اول، پرتوها، همان مجموعه خطوط هستند که برای توصیف توزیع نور استفاده شده‌اند. و در روش دوم، آن رویهٔ کروی که به آن اصطلاحاً «جبهه» یا «پیشانی» می‌گوییم، توزیع نور را توصیف کرده است. این دو توصیف کاملاً هم‌ارز هستند. «پرتو» و «جبهه» دو روش مختلف برای بیان انتشار نور می‌باشند.

برای مشخص کردن هندسی پرتوهای مختلف می‌توان در راستای هر یک از پرتوها، بردار یکه‌ای تعریف کرد که جهتش، جهت انتشار نور است (بردار انتشار پرتو). زمانی که یک پرتو به مرز جدایی می‌رسد، بسته به جهت انتشار، با زاویهٔ مشخصی در فضا به سطح مرز جدایی برخورد می‌کند. از طرف دیگر برای مشخص کردن نحوهٔ مواجههٔ پرتو با مرز جدایی، «صفحهٔ تابش» را تعریف می‌کنیم. صفحهٔ تابش، صفحهٔ متشکل از بردار سطح و بردار انتشار است. با توجه به نوع تعریف جبهه، که مشخص کنندهٔ یک سطح است، پرتو را می‌توان به شکل بردار سطح نور و صفحهٔ تابش را می‌توان به عنوان صفحهٔ متشکل از بردارِ سطح مرزِ جدایی و بردارِ سطح جبهه در نظر گرفت.

اگر چه انتشار نور در ذات خود یک پدیدهٔ زمانی است، اما در اپتیک هندسی، نمایش فضایی آن بکار می‌رود و مفهوم زمان حذف می‌شود. یعنی بجای مشخص کردن موقعیت پرتو در زمان‌های مختلف، توزیع فضایی ایستای آن مشخص می‌شود. با توجه به سرعت بالای انتشار نور، تقریباً بطور آنی شاهد رسیدن توزیع نور به حالت پایای خود هستیم. بنابراین می‌توان وضعیت پرتوها یا جبهه‌ها را در نقاط مختلف فضا مشخص کرد تا انتشار نور توصیف شود. یعنی با تصویر منجمد‌شده‌ای از انتشار نور مواجه هستیم. این تصویر تا زمانی که هدف بررسی انتشار پالسهای بسیار کوتاه نوری نباشد (چیزی که موضوع بحث اپتیک هندسی نیست)، کاملاً کفایت می‌کند. بنابراین عملاً، در نمایش هندسی انتشار نور، یا توزیع مجموعه‌ای از بردارها (پرتوها و بردارهای سطح) در محدودهٔ فضای مورد نظر نشان داده می‌شود که در نقاط مختلف پیچ و تاب می‌خورند و یا توزیع مجموعه‌ای از رویه‌های هندسی (جبهه‌ها و مرزها) که در نقاط مختلف فضا تغییر شکل می‌دهند. در این نمایش‌ها مرزهای جدایی یا بصورت بردار سطح عمود بر مرز در هر نقطه و یا بصورت رویه بیانگر مرز جدایی نمایش داده می‌شوند. ممکن است در مواردی برای وضوح بیشتر، هم پرتوها و هم جبهه‌ها نمایش داده شوند، اما دو نمایش پرتو و جبهه هم‌ارز هستند و نتایج یکسانی خواهند داشت. از طرفی، اگر چه انتشار نور در فضای سه‌بُعدی رخ می‌دهد، اما با توجه به پیچیدگی نمایش‌های سه‌بُعدی، عموماً سطح مقطع برخورد صفحات مرجعِ معینی با توزیع فضایی انتشار نور نشان داده می‌شود، یعنی با بهره گرفتن از تقارن سیستم و تعریف یک مسیر یا خط به عنوان «محور اپتیکی» و در نظر گرفتن دو صفحه متعامد بر این محور، دو تصویر دوبُعدی از توزیع نور در دو صفحه ارائه می‌شود.

به عنوان مثال، دو توصیف هندسی برای منبع نقطه‌ای (یا تصویر نقطه‌ای) داریم. توصیف اول، خطوط واگرا (یا همگرا) از (یا به) یک نقطه در فضا است و توصیف دوم، رویه‌ای کروی که مرکز آن منبع یا تصویر نقطه است. علاوه بر این، مقطع این توزیع خطوط یا رویه را با هر صفحه‌ای در فضا می‌توان مشخص کرد. در این مثال خاص، تصویر منبع نقطه‌ای در تمام صفحات، مسیرهای دایروی را به عنوان مقطع جبهه و خطوط شعاعی در آن صفحه را به عنوان مقطع پرتوها تعریف می‌کند. در حالت کلّی، به همین ترتیب برای هر دسته پرتو یا باریکه‌ٔ نامتقارنی هم می‌توان پرتوها و یا جبهه‌ها را تعریف کرد. در اپتیک هندسی، نحوهٔ تغییر پرتوها و یا تغییر جبهه‌ها در حین عبور نور از محیط‌های مختلف بررسی می‌شود.

مواجههٔ نور با مرز جدایی دو محیط

با توجه به تعاریف پرتو جبهه و در دست داشتن دو نمایش هم‌ارز برای توصیف انتشار نور، مواجههٔ نور با مرز جدایی دو محیط را به دو روش می‌توان بررسی کرد: نخست «مواجههٔ دو بردار» و دوم «مواجههٔ دو سطح». در روش اول حاصل این مواجهه یک یا چند بردار دیگر خواهد بود. در روش دوم، از برخورد دو سطح، یک یا چند سطح دیگر بدست می‌آید.

قوانین انتشار نور

قانون اول: پرتوهای نور در محیط همگن و همسانگرد، در امتداد خط مستقیم حرکت می‌کنند.

قانون دوم: نور در مواجهه با مرز جدایی دو محیط، در هر دو محیط منتشر خواهد شد.

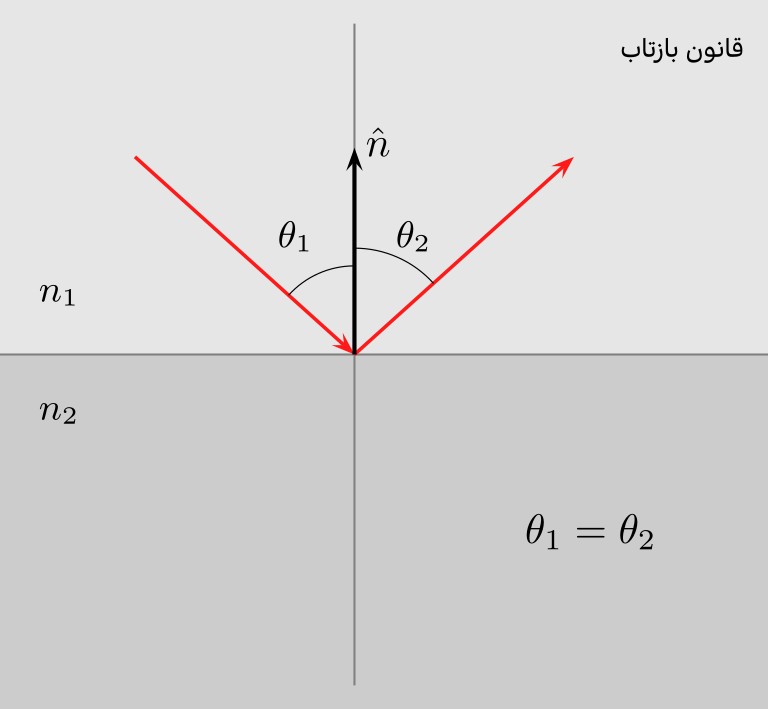
قانون سوم: قانون بازتاب

• در صفحهٔ تابش قرار دارد.
• نسبت به پرتو فرودی در طرف دیگر بردار سطح است.
• زاویه‌ای که با بردار سطح می‌سازد، برابر با زاویه‌ای است که پرتو فرودی با آن می‌سازد. به بیان ریاضی: ${\theta }_1={\theta }_2$. در اینجا ${\theta }_1$، زاویهٔ پرتو فرودی با بردار سطح و ${\theta }_2$، زاویهٔ پرتو بازتاب با بردار سطح است.

قانون چهارم: قانون شکست (قانون ابن‌سهل)

• در صفحهٔ تابش قرار دارد.
• نسبت به پرتو فرودی در طرف دیگر بردار سطح است.
• نسبت مؤلفهٔ بردار پرتو فرودی در امتداد سطح به مؤلفهٔ بردار پرتو شکستی در امتداد سطح مقدار ثابتی است. این مقدار برابر با عکس نسبت ضریب شکست دو محیط است. به بیان ریاضی نسبت سینوس زاویه‌ای که پرتو شکست با بردار سطح می‌سازد به سینوس زاویه‌ای که پرتو فرودی با بردار سطح می‌سازد، بازای همهٔ زوایای پرتو فرودی مقدار ثابتی است، یعنی $$\frac{\sin ({\theta }_1)}{\sin ({\theta }_2)}=\frac{n_2}{n_1}.$$ دراینجا ${\theta }_1$ زاویه‌ای است که پرتو فرودی با بردار سطح می‌سازد و ${\theta }_2$ زاویه‌ای که بردار شکست با بردار سطح دارد. $n_1$ و $n_2$ هم به ترتیب ضریب شکست محیط‌های اول و دوم هستند.